Edsger Wybe Dijkstra (1930 – 2002) nació en 1930 en Rotterdam, Holanda. Era hijo de Wybe Douwe Dijkstra y Brechtje Cornelia Kruyper, y tenia tres hermanos más. Su padre era professor de fisica en la escuela secundaria de Rotterdam, mientras que su madre era matemática.
De joven, asistió a la escuela secundaria de Rotterdam. Djikstra quería estudiar Derecho y asi poder representar a los Paises Bajos en las Naciones Unidas. Pero, en 1948 realizó los exámenes finales de su etapa en la escuela secundaria y sacó notas excelentes en matematicas, física, química y biología, y tanto sus padres como sus profesores intentaron persuadirle para que se decantara por una carrera de ciencias. Finalmente, decidió estudiar física teórica en la universidad de Leyden.
Tres años después, en 1951, Dijkstra vio un anuncio de la Universidad de Cambridge sobre un curso de tres semanas que trataba la programación en computadores. Se interesó mucho por este curso y decidió apuntarse, ya que lo veía como una oportunidad esta actividad, que consideraba muy ligada a su campo, la física teórica.
Aad van Wijngaarden, que era el director del Departamento de Ciencia de la Computación del Centro Matemático en Amsterdam, había hecho el mismo curso en Cambridge en el año anterior y cuando se enteró de que Dijkstra había terminado, le ofreció un puesto como programador del Centro de Matemáticas. Dijkstra aceptó el cargo desde marzo de 1952, pero sólo como una posición a tiempo parcial, ya que seguía siendo estudiante de física teórica en la Universidad de Leyden. A pesar de esto, Dijkstra empezaba a decantarse más por la programación que por la física teorica, ya que le suponía un reto mayor, al ser una rama del saber prácticamente nueva, con mucho por descubrir.
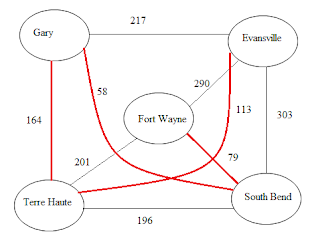
Después de haber tomado la decisión, Dijkstra completó sus estudios en física teórica en la universidad, graduándose en 1956. También en 1956, el Centro de Matemáticas de Amsterdam, en el que trabajaba completó la construcción de una nueva computadora y quería hacer una demostración pública. Para ello, Dijkstra, planteó el problema de encontrar el camino mas corto entre dos ciudades de los Países Bajos. Publicó su algoritmo, muy eficaz, que ha perdurado hasta nuestros días, y conocido popularmente como “el algoritmo de Djikstra” (o algoritmo de caminos mínimos). La idea de este algoritmo consiste en ir explorando todos los caminos más cortos que parten del vértice origen y que llevan a todos los demás vértices; cuando se obtiene el camino más corto desde el vértice origen, al resto de vértices que componen el grafo, el algoritmo se detiene.
También en 1959 fue galardonado con el doctorado de la Universidad de Amsterdam por su tesis
La comunicación con un equipo automático.
Como curiosidad, destacar que en 1957 se casó con María Debets , y tuvo dos hijos y una hija. Sin embargo, tuvo un problema en su boda porque el Juez de Paz no aceptaba “programador” como profesión para los registros, por lo que tuvo que decir que era “físico teórico” en el formulario.
Dijkstra también colaboró con el equipo de desarrollo del lenguaje de programación ALGOL-60. Hizo varias contribuciones importantes: la introducción explícita de la recursividad y la noción de ‘pila’. Dijkstra, junto con uno de sus colegas en el Centro de Matemáticas, escribió el primer compilador de ALGOL-60, que se completó en agosto de 1960.
Referencias: http://histinf.blogs.upv.es/2010/10/28/dijkstra/